What does it mean?
AGR = potential AGR [latex]\times[/latex] modifier(s)
In many plant modelling applications growth processes are modelled in such a way that maximum growth or the growth of dominant plants is reduced by mitigating agents such as the interaction with other plants and factors of the physical environment such as light, water, temperature and nutrients. Dominant plants can for example be thought of as open-grown trees growing on their own in the open landscape without interacting with any other trees so that at least stem diameter growth can be considered as maximum. This strategy is referred to as the potential-modifier approach. (AGR is absolute growth rate, see Pommerening and Muszta, 2016.)
Where does it come from?
The potential-modifier approach was first published by Newnham (1964) and Botkin et al. (1972) as part of empirical and so-called gap models.
Why is it important?
Potential growth defines an upper limit of growth for a given species on a given site. This avoids unrealistic model estimations, as can be the case when estimating AGR directly from plant size, interaction and factors of the abiotic environment. Usually only the model parameters of the function defining potential growth change when adapting the model to new species and sites whilst the parameters relating to the modifiers stay the same. This increases the robustness of the overall growth model and allows easier adaptations.
How can it be used?
Measurements from the above-mentioned open-grown trees can be used for defining potential AGR. However, since this involves substantial additional sampling efforts, another strategy is to apply quantile regression (Koenker and Park, 1994; Cade and Noon, 2003) to the data collected for parametrisation. Quantile regression is not so different from conventional regression. Instead of fitting functions of the usual 0.5-quantile of the observed data (mean regression), larger or smaller quantiles are selected. For the application to the potential-modifier approach usually upper quantiles of 0.95 or 0.975 are used.
For example, assuming a dependency on size tree stem-diameter, AGR can be described using the first derivative of the Chapman-Richards growth function (Pienaar and Turnbull, 1973; see also my earlier blog on this function):
[latex]y’ = A k p e^{-ky} (1 – e^{-ky})^{p – 1}[/latex],
where y in this case is tree stem diameter but otherwise could be any plant size characteristic. A, k and p are model parameters.
R code
In R, it is quite straightforward to apply quantile regression thanks to the quantreg package. In preparation AGR and size data should be compiled in a common data frame. Then we install and load the quantreg package:
install.packages("quantreg", dep = T)
library(quantreg)
Next we define the AGR function to be used for describing potential growth and this we again use the aforementioned first derivative of the Chapman-Richards growth function, where time is exchanged for size (stem diameter dbh in this case):
dpot <- function(dbh, xA, xk, xp) {
return(xA * xk * xp * exp(-xk * dbh) * (1 - exp(-xk * dbh)) ^
(xp - 1))
}
Finally we can use the quantile regression routine, which in turn uses function dpot:
nlsout <- nlrq(AGR ~ dpot(dbh, A, k, p), data = TreeList,
start = list(A = 54.1, k = 0.01, p = 1.19), tau = 0.975,
trace = TRUE)
From the syntax we can see that the difference to common regression procedures such as nls is minimal. The main difference is parameter [latex] \tau [/latex] which defines the quantile. A model summary can be obtained in the same way as from nls which also allows retrieving the model parameters:
summary(nlsout)
A <- summary(nlsout)$coefficients[1]
k <- summary(nlsout)$coefficients[2]
p <- summary(nlsout)$coefficients[3]
And here is an example result:
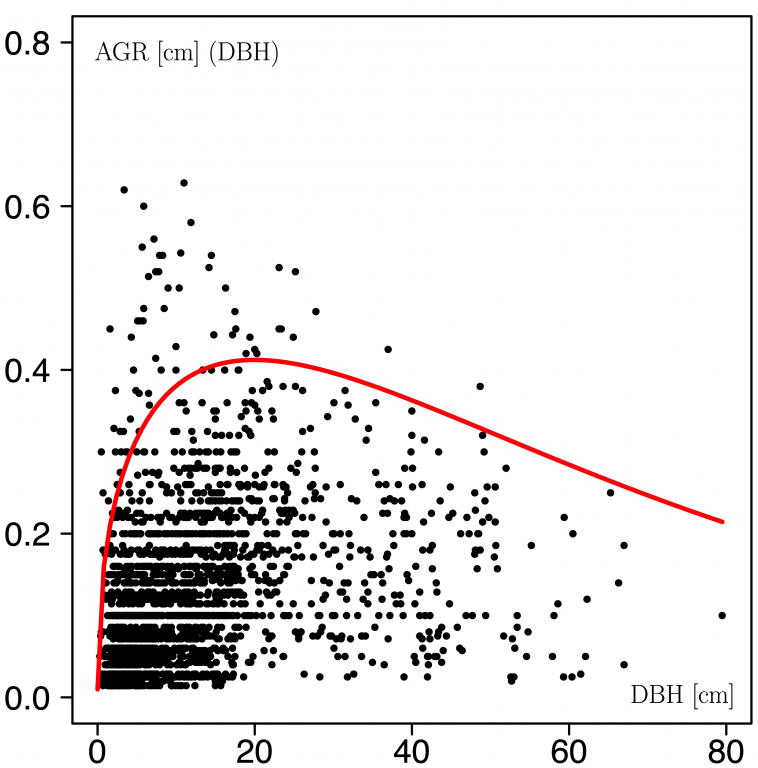
Cade and Noon (2003) noted that quantile regression also has a general place in data analysis providing a more complete view of possible causal relationships between variables in ecological processes, where mean regression techniques would fail to identify relationships between explanatory and response variables. The additional advantage is that one can directly estimate rate parameters for changes in the quantiles of the distribution responses conditional on the predictor variables.
Literature
Botkin, D. B., Janak, J. F., Wallis, J. R., 1972. Some ecological consequences of a computer model of forest growth. The Journal of Ecology 60: 849.
Cade, B. S., Noon, B. R., 2003. A gentle introduction to quantile regression for ecologists. Frontiers in Ecology and the Environment 1: 412-420.
Koenker, R., Park, B. J., 1994. An interior point algorithm for nonlinear quantile regression. Journal of Econometrics 71: 265-283.
Pienaar, L. V. and Turnbull, K. J., 1973. The Chapman-Richards generalization of von Bertalanffy’s growth model for basal area growth and yield in even-aged stands. Forest Science 19: 2-22.
Pommerening, A. and Muszta, A., 2016. Relative plant growth revisited: Towards a mathematical standardisation of separate approaches. Ecological Modelling 320: 383-392.
Newnham, R. M., 1964. The development of a stand model for Douglas fir. Ph.D thesis, University of British Columbia, Vancouver, 201p.