The Chapman-Richards growth function

[latex]{\LARGE y(t) =y_\text{max} [1 – e^{-kt}]^p}[/latex]

 

What does it mean?

Growth functions in general describe the change in size of an individual or population with time (Burkhart and Tomé, 2012). Assume that [latex]y(t)[/latex] is a tree growth variable, e.g. tree total height or tree volume, and  [latex]y_\text{max}[/latex] is the maximum value this growth variable can take (in absolute terms for a given species in general or for a given species on a given site) then the term [latex][1 – e^{-kt}]^p [/latex] is a modifier reducing the maximum growth variable to its current state at time [latex]t[/latex].  [latex]k[/latex] is an empirical growth parameter scaling the absolute growth rate. The empirical parameter [latex]p[/latex] is related to catabolism (destructive metabolism), which is said to be proportional to an organism’s mass. Therefore it is often restricted to a value of three for theoretical, biological reasons.

The Chapman-Richards growth function can be applied to both, individual organisms as was well as to the growth of whole populations and describes cumulative growth over time. As such the function has an inflection point and an upper asymptote at  [latex]y_\text{max}[/latex] reflecting a so-called sigmoid growth curve typical of growth processes, which are influenced by biotic and abiotic factors.

Where does it come from?

The Chapman-Richards growth function is based on the seminal work by Bertalanffy for animal growth and was published by Richard in 1959 and Pienaar and Turnbull (1973) introduced it to forestry applications. The model has a reputation of being very flexible on the slight expense of biological realism. It is valued for its accuracy, although there can be problems in the process of parameter estimation when  [latex]p[/latex] is allowed to vary (Clutter et al., 1983; Pienaar and Turnbull, 1973; Zeide, 1933).

Why is it important?

The Chapman-Richards growth function has been a popular model for describing the growth of various tree and forest stand growth variables, e.g. tree and stand height, diameter at breast height, basal area and volume. As such it has been and is still widely used in many empirical forest growth simulators, particularly where the accuracy of model prediction is crucial (Zeide, 1933). The Chapman-Richards growth function has been used extensively to model site index development, i.e. the mean height development of the most dominant trees of a forest as a population characteristic for describing site quality (Burkhart and Tomé, 2012), leading to a so-called polymorphic height growth model.

How can it be used?

Assume you have access to sample data providing several combinations of a growth variable, e.g. tree height, and age. Using nonlinear regression methods you can estimate the parameters of the Chapman-Richards growth function. After estimating the growth parameters the model can be used for interpolation and for predicting past and future growth.

Absolute growth rate (AGR) is essentially the first derivative of the Chapman-Richards growth function:

[latex]y'(t) =y_\text{max} k p e^{-kt} (1 – e^{-kt})^{p – 1}[/latex]

 

The AGR function can be employed to model current annual increment or instantaneous growth. For relative growth rate (RGR) we lose one model parameter (Pommerening and Muszta, 2016) and the function terms simplifies to

[latex]p(t) =k p (1 – e^{-kt})^{-1}[/latex].

Also the algebraic difference form (ADA) of the Chapman-Richards growth function is often applied (Burkhart and Tomé, 2012),

[latex]y(t) = y(t – \Delta t) [\frac{1 – e^{-kt}}{1 – e^{-k(t – \Delta t)}}]^p[/latex],

where the fracture constitutes a growth multiplier (Pommerening and Muszta, 2016) and the aymptote [latex]y_\text{max}[/latex] disappears. The algebraic difference form allows estimating the current value of a growth variable from a value in the past (anamorphic model).

R code

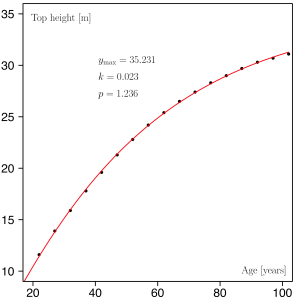
In R it is quite straightforward to estimate the parameters of the Chapman-Richards growth function through nonlinear regression. First we need some sample data and I have taken pairs of top height (the mean height of dominant trees, a population characteristic) and the corresponding age (assuming an even-aged forest) from a British yield table. In more interesting applications, similar data would naturally stem from field observations.

# Using some data from the British yield table for Scots pine, YC 14.
topHeight <- c(8.9, 11.6, 13.9, 15.9, 17.8, 19.6, 21.3, 22.8, 24.2, 
+ 25.4, 26.5, 27.4, 28.3, 29.0, 29.7, 30.3, 30.7, 31.1)
age <- c(17, 22, 27, 32, 37, 42, 47, 52, 57, 62, 67, 72, 77, 82, 87, 
+ 92, 97, 102)

Then we load a package for robust regression (as we know that the Chapman-Richards model can sometimes “play up”).

library(robustbase)

Finally we enter the actual regression code specifying the model, the data and the start parameters. The summary command provides the regression outputs including the estimated model parameters. (Parameter  [latex]A[/latex] corresponds to parameter  [latex]y_\text{max}[/latex] in the above equation.)

nlsout <- nlrob(topHeight ~ A * (1 - exp(-k * age))^p, data = 
data.frame(age, topHeight), start = list(A = 83, k = 0.03, p = 4), 
trace = TRUE)
summary(nlsout)
summary(nlsout)$coefficients[1 : 3]

It is always a good idea to check the value of parameter  [latex]y_\text{max}[/latex] against the maximum value of the growth variable: Both values shouldn’t be very far off, because [latex]y_\text{max}[/latex] is the upper asymptote of the growth function.

Literature

Burkhart, H. and Tomé, M., 2012. Modeling forest trees and stands. Springer, Dordrecht.

Clutter, J. L, Fortson, J. C., Pienaar, L. V., Brister, G. H. and Bailey, R. L., 1983. Timber management. A quantitative approach. John Wiley & Sons, New York.

Pienaar, L. V. and Turnbull, K. J., 1973. The Chapman-Richards generalization of von Bertalanffy’s growth model for basal area growth and yield in even-aged stands. Forest Science 19: 2-22.

Pommerening, A. and Muszta, A., 2016. Relative plant growth revisited: Towards a mathematical standardisation of separate approaches. Ecological Modelling 320: 383-392.

Zeide, B., 1993. Analysis of growth equations. Forest Science 39: 594-616.